4  Probability and Distributions

I have studied many languages-French, Spanish and a little Italian, but no one told me that Statistics was a foreign language. – Charmaine J. Forde

4.1 From description to inference

Up to this point, we’ve focused on experimental design and descriptive statistics: how to collect data and how to summarize it with graphs and averages. But statistics is more than description. Its power is in inference, using limited data to say something about a broader population. Inference relies on two foundations: probability theory and the behavior of samples from distributions.

4.2 Probability vs. Statistics

Probability and statistics are closely related but not the same.

Probability starts with a known model of the world and asks: what kinds of data are likely?

• Example: What is the chance of flipping 10 heads in a row with a fair coin?
• Example: What is the chance of drawing five hearts from a shuffled deck?

Here, the model is known (fair coin, fair deck). Data are imagined.

Statistics starts with data and asks: what model of the world generated these data?

• Example: If a coin comes up heads 10 times in a row, is it fair?
• Example: If five cards in a row are hearts, was the deck shuffled?

Here, the data are known. The model is what we want to learn about.

Note

Shortcut: - Probability = model → data. - Statistics = data → model.

4.3 What does probability mean?

Statisticians agree on the rules of probability but not always on what the word itself means. In everyday life we’re comfortable saying something is “likely” or “unlikely,” but the formal meaning varies.

Imagine a soccer game between Arsenal and West Ham. You say Arsenal has an 80% chance of winning. That could mean:

1. Long-run frequency: if the teams played many times, Arsenal would win ~8 out of 10.

2. Betting odds: you’d only take a wager if payoffs reflected an 80/20 split.

3. Subjective belief: your confidence in Arsenal is four times stronger than in West Ham.

All three interpretations follow the same rules but reflect different philosophies.

For our purposes, the math works the same either way. In this course we’ll use the frequentist view, so you can think of probability as the long-run proportion of times an event would occur if you could repeat the process many times (that’s #1 above).

4.4 Basic probability theory

At the core of probability theory is the idea of a distribution: a set of possible outcomes and their probabilities.

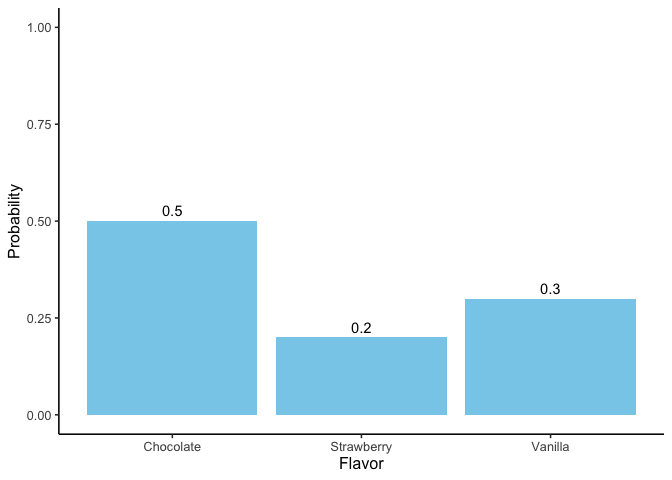
Suppose we track which ice cream flavor a customer chooses: chocolate, vanilla, or strawberry. Each choice is an elementary event, and the set of all possible events is the sample space, \(S\):

\(S = {\text{chocolate}, \text{vanilla}, \text{strawberry}}\)

If we record how often each flavor is chosen, we might estimate the following probabilities:

Flavor Probability:

• Chocolate \(P(\text{chocolate})=0.5\)

• Vanilla \(P(\text{vanilla})=0.3\)

• Strawberry \(P(\text{strawberry})=0.2\)

These probabilities form a distribution. Each value lies between 0 and 1, and together they sum to 1.

Figure 4.1: A simple probability distribution: the probabilities for three flavors must add to 1.

Non-elementary events

We can also define events that group multiple outcomes.

For example, let \(A=\) “not chocolate.” Then:

\[P(A) = P(vanilla) + P(strawberry) = 0.5\]

4.5 Rules of Probability

Some basic rules follow from this framework. Let’s consider a sample space \(X\) that consists of elementary events \(x\), and two non-elementary events, which we’ll call \(A\) and \(B\).

Here are our rules:

English	Notation	Formula
not A	\(\neg A\)	\(P(\neg A) = 1 - P(A)\)
A and B	\(A \cap B\)	\(P(A \cap B) = P(A\mid B)\,P(B) = P(B\mid A)\,P(A)\)
A or B	\(A \cup B\)	\(P(A \cup B) = P(A) + P(B) - P(A \cap B)\)
A given B	\(A \mid B\)	\(P(A \mid B) = \dfrac{P(A \cap B)}{P(B)}\)

These rules look abstract at first, but they are just formal ways of describing common-sense situations. Let’s work through them step by step with our ice cream example. We’ll assign probabilities to each flavor and then show how the rules play out with real numbers. That way, the notation is always tied to something you can picture.

Let’s add a fourth flavor and assign some probabilities:

Flavor Probability:

• Chocolate \(P(\text{chocolate})=0.4\)

• Vanilla \(P(\text{vanilla})=0.3\)

• Strawberry \(P(\text{strawberry})=0.2\)

• Rocky Road \(P(\text{rocky road})=0.1\)

Notice these add to 1, as they must.

We’ll have two non-elementary events, \(A\) and \(B\), defined as:

\(A = (\text{chocolate, vanilla, strawberry})\)

\(B = (\text{chocolate, rocky road})\)

4.5.1 Not \(A\)

\(A = (\text{chocolate, vanilla, strawberry})\)

\(P(A) = 0.4 + 0.3 + 0.2 = 0.9\)

So, \(P(\neg A) = 1 - P(A) = 1 - 0.9 = 0.1\)

Explanation: This adds up logically. The chance of not choosing chocolate, vanilla, or strawberry is equal to the chance of Rocky Road.

4.5.2 \(A\) and \(B\) (the intersection)

Think of and as meaning “both at once.” For probabilities, that translates into the overlap of the two events.

• The only overlap between \(A\) and \(B\) is chocolate: \(A \cap B = (\text{chocolate})\)

• The intersection \(A \cap B\) contains only chocolate, and its probability is \(0.4\).

• So \(P(A \cap B) = 0.4\)

To reiterate: And means overlap, not “add the probabilities together.”

4.5.3 \(A\) or \(B\) (the union)

Or in probability is inclusive: it means “in A, or in B, or in both.”

• If we combine everything in either set, we get all four flavors.

• \(A \cup B = (\text{chocolate, vanilla, strawberry, rocky road})\)

• That’s the whole sample space, so \(P(A \cup B) = 1\).

• So \(P(A \cup B) = 1\).

To reiterate: or covers everything in either group. We subtract the overlap ($A B$) so we don’t double-count it.

4.5.4 Conditional probability

Suppose we want \(P(B \mid A)\): the probability of choosing \(B\) (chocolate or rocky road) given that we already know the choice was from \(A\) (chocolate, vanilla, strawberry).

By the rule,

\[P(B \mid A) = \frac{P(A \cap B)}{P(A)} = \frac{0.4}{0.9} \approx 0.44\]

Explanation: Given the choice is from the \(A\) group, the only overlap with \(B\) is chocolate. So there’s about a 44% chance the flavor is chocolate.

4.6 Probability Distributions

A probability distribution is a rule that assigns probabilities to all possible outcomes of a random variable. Many distributions exist, but this book mostly uses five: Binomial, Normal, \(t\), χ² (“chi-square”), and \(F\). We’ll focus on Binomial and Normal here; the others appear when we do inference.

The binomial and the normal represent two kinds of distributions: discrete and continuous.

• Discrete distributions assign probabilities to distinct outcomes.

• Continuous distributions describe ranges of values, where probabilities are measured as areas under a curve.

4.6.1 The binomial distribution (discrete)

The binomial distribution models the number of “successes” in a fixed number of independent trials.

• A trial is a single attempt with two possible outcomes (success or failure).
• The success probability is the chance of success on any one trial, usually written as \(\theta\).
• The size parameter \(N\) is the number of trials.
• The random variable \(X\) is the number of successes observed in those \(N\) trials.

We write this as:

\(X \sim \text{Binomial}(N, \theta)\)

For example, if you flip a fair coin 20 times (\(N=20\), \(\theta=0.5\)), the binomial distribution tells you the probability of getting 0 heads, 1 head, 2 heads … all the way up to 20 heads. The bars of the distribution in Figure 4.2 show the probability of each outcome, and the total always sums to 1.

Figure 4.2: Binomial probabilities for X ~ Binomial(N = 20, θ = 0.5). Bars show P(X = x).

Two common queries

1. Exact probability. For example, the chance of exactly 4 heads: \(P(X=4)\)

dbinom(x = 4, size = 20, prob = 0.5)
#> [1] 0.004620552

The probability is about \(0.5\)%.

2. Cumulative probability. For example, \(P(X \leq 4)\):

pbinom(q = 4, size = 20, prob = 0.5)
#> [1] 0.005908966

The probability is about \(0.6\)%

The probability is slightly higher here, because it also includes the probability we could get 3, 2, or 1 heads as well.

Note

R’s distribution helpers (for every distribution):

• d* = exact probability (PDF)
• p* = cumulative probability \(P(X \le q)\)
• q* = quantile (inverse of p*)
• r* = random draws

For binomial: dbinom, pbinom, qbinom, rbinom. For discrete distributions, some percentiles don’t exist exactly; qbinom returns the smallest x with P(X x) p.

4.6.2 The normal distribution (continuous)

The normal distribution describes variables that can take on a wide range of values, clustered around a central point. The normal distribution is our most important distribution. It’s also sometimes called a Gaussian distribution or a bell curve.

• The mean \(\mu\) is the center of the distribution.
• The standard deviation \(\sigma\) measures spread: how tightly or widely values are clustered around the mean.
• The random variable \(X\) represents the outcome, which can be any real number.

We write this as:

\(X \sim \text{Normal}(\mu, \sigma)\)

It looks like Figure 4.3.

Figure 4.3: Standard normal Probability Distribution Function (PDF), where μ = 0, σ = 1. For continuous variables, probabilities are areas under the curve.

Note

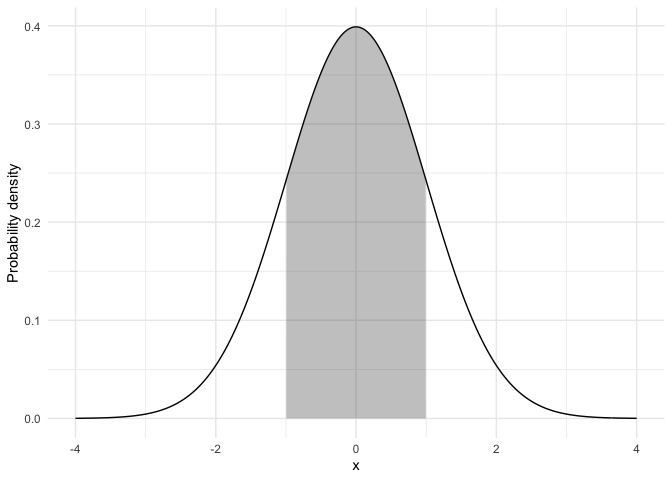
For continuous distributions: - Point probability = 0 - Probability = area under curve

Changing \(\mu\) shifts the curve left/right; changing \(\sigma\) widens/narrows it (area always = 1).

For continuous distributions \(P(X = x) = 0\); instead, we compute \(P(a \le X \le b)\) as the area between \(a\) and \(b\).

See Figure 4.4 for an illustration.

This leads to a key property of the normal distribution (explored further in the Z-scores section):

68–95–99.7 rule:

• ~68% of values fall within 1σ of the mean
  

• ~95% fall within 2σ
  

• ~99.7% fall within 3σ

Figure 4.4: Shaded area shows P(−1 ≤ X ≤ 1) ≈ 0.68 for X ~ Normal(0,1).

Two common queries

1. Probability of being below a value, e.g. \(P(X \leq 1.64)\) for \(X \sim \text{Normal}(0,1)\)

pnorm(q = 1.64, mean = 0, sd = 1)
#> [1] 0.9494974

In a normal distribution with a mean of 0 and standard deviation of 1, the probability the value is less than or equal to 1.64 is about 95%.

2. Value for a percentile, e.g. the 97.5th percentile:

qnorm(p = 0.975, mean = 0, sd = 1)
#> [1] 1.959964

Takeaway: For continuous variables, use areas (via pnorm/qnorm), not bar heights.

4.6.3 What’s probability density?

For continuous distributions like the normal, probabilities work differently than in the discrete case. You cannot ask for the probability of one exact value (e.g., \(P(X = 23)\)), because the answer is essentially zero. Instead, we calculate the probability of being in a range, such as \(22.5 \leq X \leq 23.5\).

This is why the \(y\)-axis of a normal curve is labelled probability density. The height of the curve at a point, \(p(x)\), is not itself a probability. Instead, probabilities come from the area under the curve between two values. For example, about 68% of values from a standard normal fall between −1 and 1, because the area between −1 and 1 is 0.68.

In R, functions like dnorm() return the density (the curve’s height), while pnorm() and qnorm() work with cumulative probabilities and quantiles, which are usually more useful for applied problems.

4.7 Summary of Probability

In this section we introduced the building blocks of probability, with an emphasis on the parts most relevant for statistics.

• What probability means: We use the frequentist view—probability as the long-run proportion of times an event occurs.

• Distributions: A probability distribution assigns probabilities to all possible outcomes of a random variable. For discrete variables (like coin flips), probabilities are attached to each outcome; for continuous variables (like exam scores), probabilities come from areas under a curve.

• Rules of probability: Complements, intersections (and), unions (or), and conditional probabilities all follow from the basic distribution framework.

• Key distributions:

  • Binomial—counts successes across \(N\) independent trials.
  • Normal—describes continuous outcomes centered at a mean, with spread determined by the standard deviation.
  • Others (\(t\), \(\chi^2\), \(F\)) appear later when we turn to inference.

Takeaway: probability provides the language and tools that make statistical inference possible. Once we understand how outcomes behave under these distributions, we can ask questions about samples, uncertainty, and whether results are surprising enough to change what we believe about the world.

4.8 Samples, populations and sampling

Descriptive statistics summarize what we do know. Inferential statistics aim to “learn what we do not know from what we do.” The central questions are: what do we want to learn about, and how do we learn it? Introductory statistics typically divides inference into two big ideas: estimation and hypothesis testing. This chapter introduces estimation, but first we need to cover sampling. Estimation only makes sense once you understand how samples relate to populations.

Sampling theory specifies the assumptions on which statistical inferences rest. To talk about making inferences, we must be clear about what we are drawing inferences from (the sample) and what we are drawing inferences about (the population).

In almost every study, what we actually have is a sample—a finite set of data points. We cannot survey every voter in a country or measure every tree in a forest. Earlier, our goal was just to describe the sample. Now we turn to how samples can be used to generalize.

4.8.1 Defining a population

A sample is tangible: it is the dataset you can open on your computer. A population, by contrast, is the (usually much larger) set of all possible individuals or observations you want to draw conclusions about. In an ideal world, researchers would start with a clear definition of the population of interest, since that shapes how a study is designed. In practice, the population is often only loosely defined. Still, the basic idea is simple: the sample should represent some broader population we care about.

4.8.2 Simple random samples

The sample–population relationship depends on the procedure used to select the sample. This is the sampling method, and it matters.

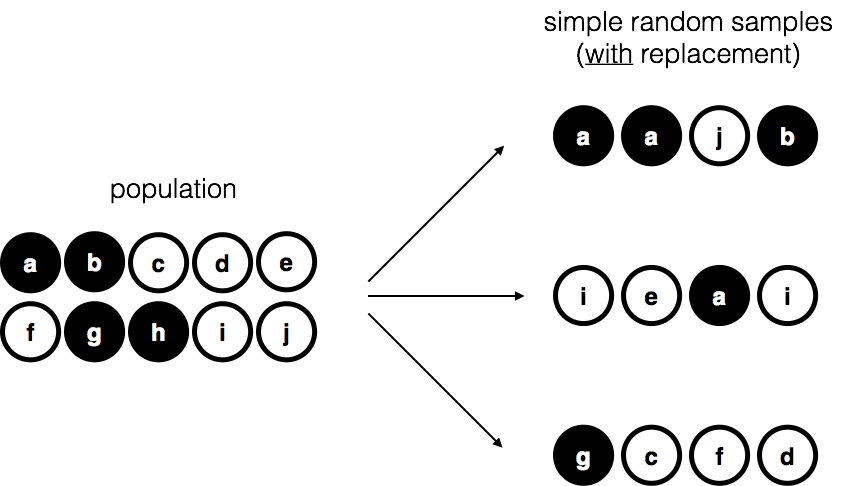
Suppose we have a bag with 10 chips, each uniquely labeled, some black and some white. This bag is the population. If we shake the bag and draw 4 chips without replacement, each chip has the same chance of being selected. This is a simple random sample.

Figure 4.5: Simple random sampling without replacement from a finite population

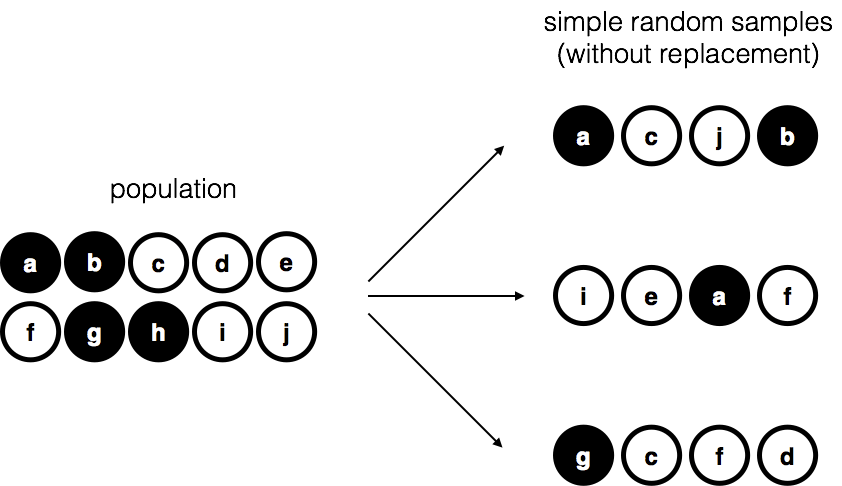
Now imagine a different procedure: someone peeks inside and deliberately picks only black chips. That is a biased sample. The difference is critical. With a random sample, we can use statistical tools to generalize from the sample to the population; with a biased sample, we cannot.

Figure 4.6: Biased sampling without replacement from a finite populations.

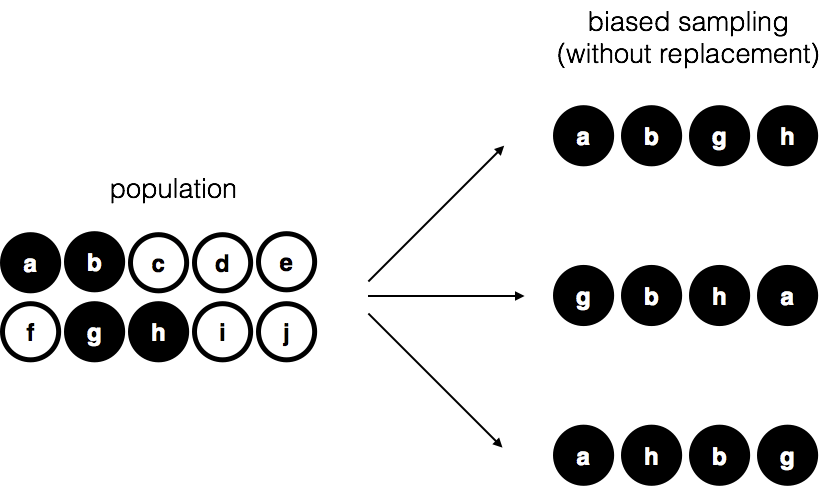
Another variation is to draw chips with replacement—each chip is returned to the bag before the next draw. In practice, most studies are “without replacement,” but much of statistical theory assumes replacement. When the population is large, the difference is negligible.

Figure 4.7: Simple random sampling with replacement from a finite population.

4.8.3 Random and non-random samples in practice

Random samples are the gold standard, and in many areas of environmental science they are common: inventory plots, transects, and monitoring networks are usually designed with probability-based methods. Still, many studies rely on modified approaches:

• Stratified sampling divides the population into subgroups (strata) and samples within each. This ensures representation of small but important groups, such as rare habitat types.
• Opportunistic or logistically constrained sampling selects cases that are accessible or already monitored. These are not random, but they are common in practice when budgets, terrain, or historical networks limit where data can be collected. .

4.8.4 How much does it matter if you don’t have a random sample?

The short answer: it depends. Stratified sampling, while biased by design, is often useful and correctable with statistical adjustments. Opportunistic samples can be acceptable if the bias is unlikely to affect the phenomenon being studied. For example, if you want to study tree growth rates, sampling only trees on one side of a valley may or may not be problematic, depending on whether the valley side influences growth.

The key is to consider whether the way you sampled could plausibly distort the conclusions. When designing your own studies, aim for sampling methods that are as appropriate as possible for the population of interest. And when critiquing others, be specific about how a sampling choice might bias results, rather than simply noting that it is not random.

4.8.5 Population parameters and sample statistics

So far we have talked about populations the way a scientist might: a group of people, a stand of trees, a set of rivers. Statisticians formalize this idea by treating a population as a probability distribution—the abstract source from which data are drawn.

For example, suppose daily coffee consumption in adults follow an approximately normal distribution with mean \(\mu - 2\) cups/day and standard deviation \(\sigma = 1\) cup/day. These are the population parameters.

Figure 4.8: The population distribution of daily coffee consumption (a) and two random samples: one of size 100 (b) and one of size 10,000 (c).

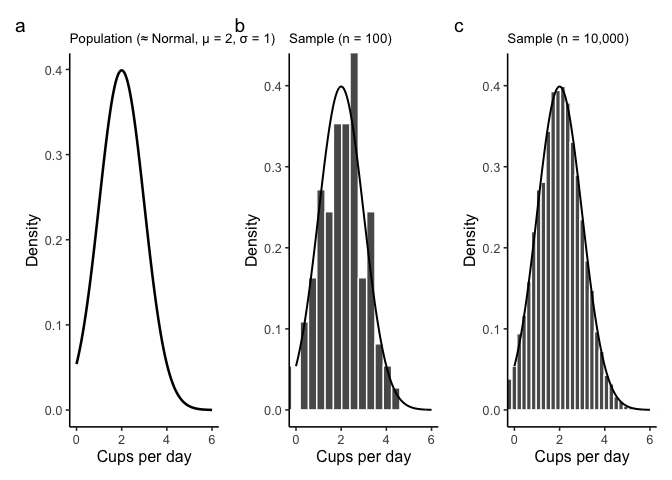
Now suppose we take a random sample of 100 adults. The histogram in panel (b) of Figure 4.8 shows that the sample resembles the population distribution, but not perfectly. The sample mean might be 1.9 cups and the sample standard deviation 1.1—close to, but not exactly, the population values.

These are sample statistics: numbers we calculate from the data in hand. They approximate the population parameters, which describe the entire distribution. The central problem of inference is how to use sample statistics to estimate population parameters, and how much confidence we can place in those estimates.

4.9 The law of large numbers

In the last section we compared a small sample of coffee drinkers (\(n=100\)) to a much larger sample (\(n=10{,}000\)). The difference was clear: the larger sample produced a histogram that looked much closer to the true population distribution. The sample mean and standard deviation were also much closer to the population values (\(\mu = 2\), \(\sigma = 1\) cups/day).

This illustrates the law of large numbers. Informally: larger samples give better information. More precisely, as the sample size grows, the sample mean \(\bar{X}\) converges toward the population mean \(\mu\). Symbolically:

\[ N \to \infty \quad \Rightarrow \quad \bar{X} \to \mu \]

Although easiest to see with the mean, the law applies to many sample statistics: proportions, variances, correlations, and more. The guarantee is that, with enough data, the statistics you calculate from a sample will hover ever closer to their population counterparts.

The idea is obvious enough that Jacob Bernoulli, who first formalized it in 1713, remarked that “even the most stupid of men” already know it by instinct. His phrasing hasn’t aged well, but the insight remains correct: averaging over more observations reduces the “danger of wandering from one’s goal.”

In practice, this means any single sample statistic will be off the mark, but if we keep collecting data, those statistics will tend to get closer and closer to the true population parameters. The law of large numbers is one of the fundamental guarantees that makes statistical inference possible.

4.10 Sampling distributions and the central limit theorem

The law of large numbers tells us that with enough data, our sample mean will get close to the population mean. But in practice, we never have infinite data. What we need is a way to understand how the sample mean behaves with finite samples. This is where the sampling distribution of the sample means comes in.

4.10.1 Sampling distribution of the sample means

The phrase is clunky, but the idea is straightforward.

• A sample mean is just the average of one sample.
  
• A sampling distribution is what you get when you take many samples, compute the mean for each, and then look at the distribution of those means.

So the sampling distribution of the sample means is simply the distribution formed by repeating your study many times and collecting all those sample averages.

Why is this useful? Because it tells us how much the sample mean varies from sample to sample, and how close we can expect it to be to the population mean.

4.10.2 Seeing the pieces

We can build this step by step:

1. Start with a distribution to sample from.
   
2. Draw repeated random samples of the same size \(n\).
   
3. Compute the mean of each sample.
   
4. Plot those means in a histogram.

For example, suppose we draw numbers from a uniform distribution on 1 to 10: Figure 4.9.

Figure 4.9: A uniform distribution illustrating the probabilites of sampling the numbers 1 to 10. In a uniform distribution, all numbers have an equal probability of being sampled, so the line is flat indicating all numbers have the same probability

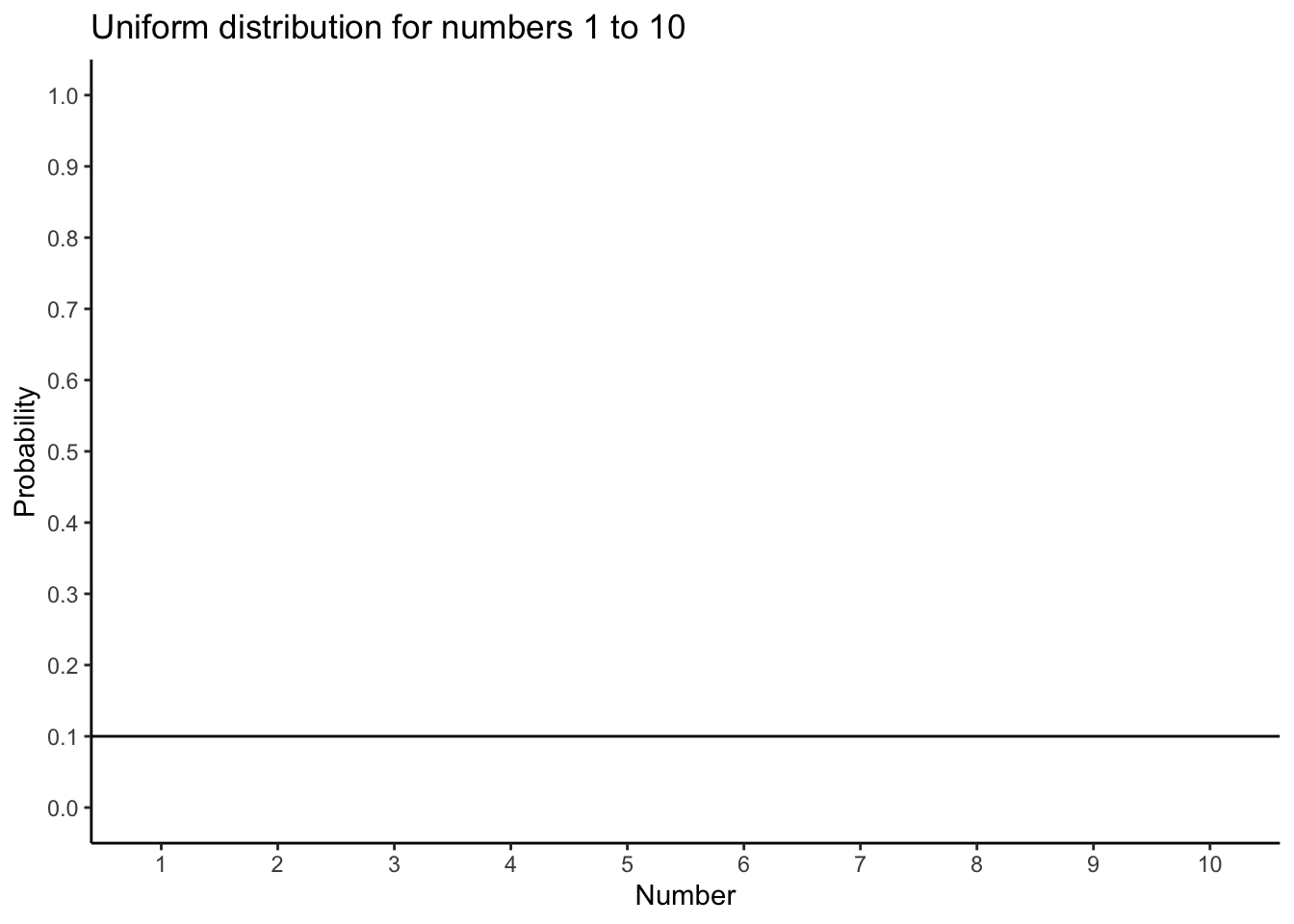
Individual samples of size 20 look very different from each other, but their means cluster near 5.5 (the population mean).

If we repeat this thousands of times and plot all the sample means, we get a new distribution: the sampling distribution of the sample means. It is centered on 5.5, but spread out because of sampling variation.

Figure 4.10: A histogram showing the sample means for 10,000 samples, each size 20, from the uniform distribution of numbers from 1 to 10. The expected mean is 5.5, and the histogram is centered on 5.5. The mean of each sample is not always 5.5 because of sampling error or chance

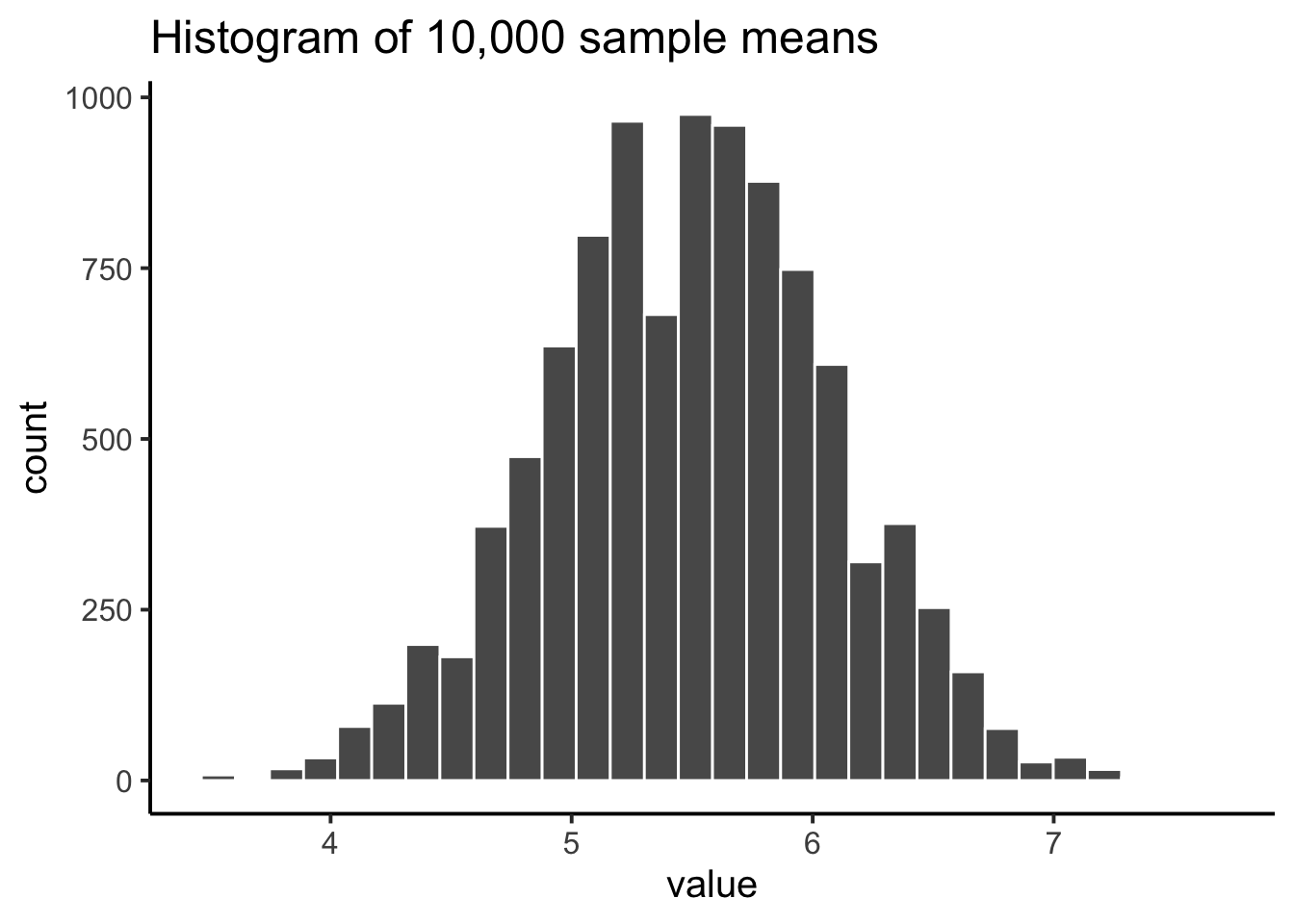
We had a uniform distribution originally, but Figure 4.10 does not look like a uniform distribution. This is key takeaway: the histogram of sample means does not look like the original uniform distribution. Instead, it has its own shape and variability. That fact leads directly to the central limit theorem, which we’ll introduce next.

4.10.3 Beyond the mean

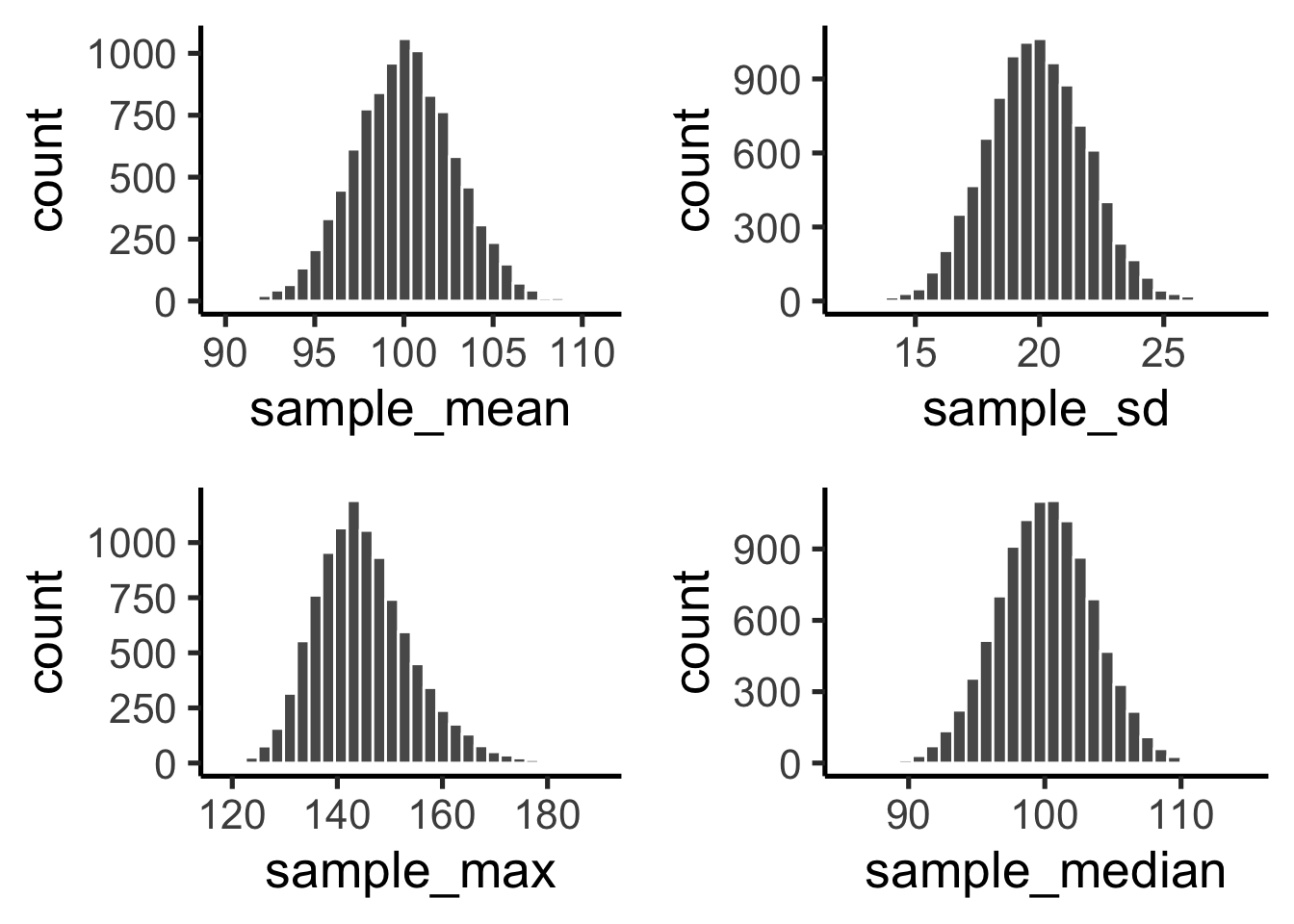
Although we’ve focused on means, the same idea applies to any statistic—medians, standard deviations, maximum values, and so on. Each has its own sampling distribution, which describes how that statistic behaves across repeated samples. To illustrate, suppose we draw many samples of size \(n=50\) from a normal distribution with mean 100 and standard deviation 20. For each sample we compute the mean, standard deviation, maximum, and median, then plot the histograms of these values (Figure 4.11).

The sample mean is just the most important case, because it underpins much of classical inference.

Figure 4.11: Each panel shows a histogram of a different sampling statistic

4.11 The central limit theorem

So far, you’ve seen that sample means vary from one sample to the next, and that their variability shrinks as sample size grows. The sampling distribution of the mean is just the distribution you get if you compute the mean from many different samples of the same size.

Intuitively: - Small samples → sample means bounce around more → wide sampling distribution. - Large samples → sample means are more stable → narrow sampling distribution.

Figure 4.12 animates this idea. Each panel shows samples of size 10, 50, 100, or 1000 drawn from a normal distribution (red line). Grey bars show the sample itself, the red line marks that sample’s mean, and the blue histogram shows the distribution of sample means across many repetitions. Notice how the blue distribution shrinks around the population mean as \(n\) increases.

Figure 4.12: Simulation of samples (grey), their means (red line), and the sampling distribution of the mean (blue). As sample size grows, the distribution of sample means narrows and centers on the population mean.

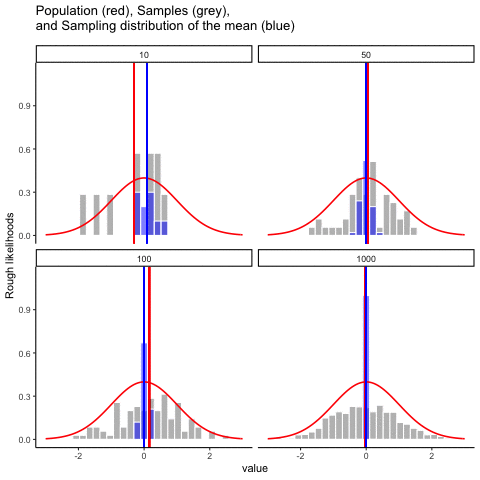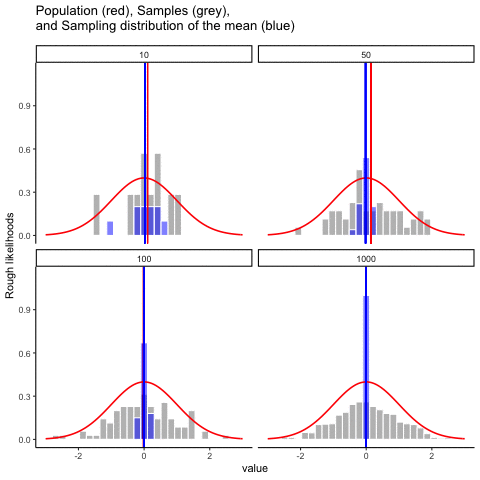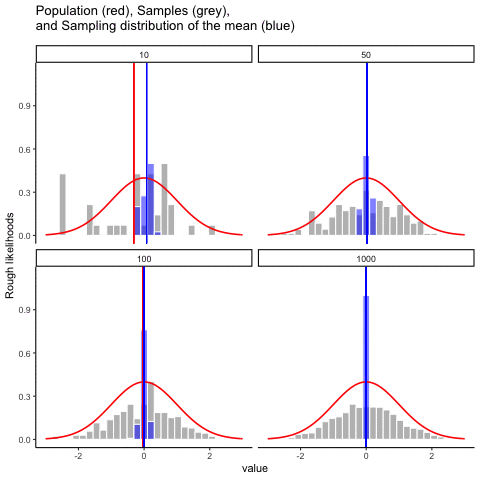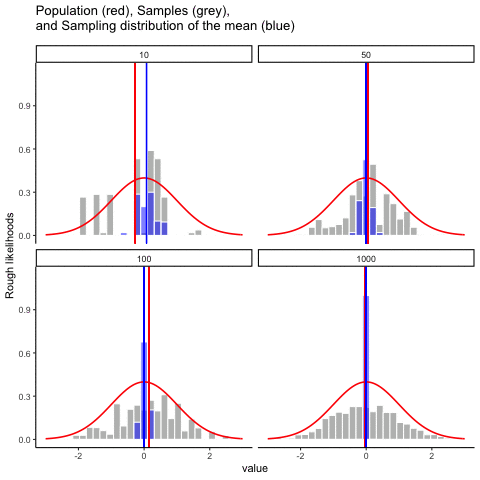
So, the sampling distribution of the mean is itself a distribution, with its own variability. When the sample size is small, the distribution of sample means is wide; when the sample size is large, it is narrow. The standard deviation of this sampling distribution has a special name: the standard error (SE). In this context, it is the standard error of the mean. As you can see in the animation, as the sample size \(N\) increases, the SE decreases.

But there’s more. The central limit theorem tells us three powerful facts about the sampling distribution of the mean:

1. Its mean equals the population mean, \(\mu\).

2. Its standard deviation equals the population \(\sigma\) divided by \(\sqrt{N}\):

\[\text{SEM} = \frac{\sigma}{\sqrt{N}}\]

3. Its shape approaches normal as \(N\) grows — no matter what the shape of the population is.

Together, these three facts form our practical version of the central limit theorem (CLT). The first fact, that sample means converge to the population mean, comes from the law of large numbers. The second formalizes how the SE shrinks with larger \(N\). And the third shows why the normal curve appears so often: the distribution of sample means tends toward normality, even when the underlying data are skewed or flat.

The full CLT is mathematically more general and has a complicated proof, but for our purposes these three results capture what we need. To see the third point in action, let’s look at histograms of sample means drawn from different underlying distributions. Remember: these are distributions of sample means, not of individual observations.

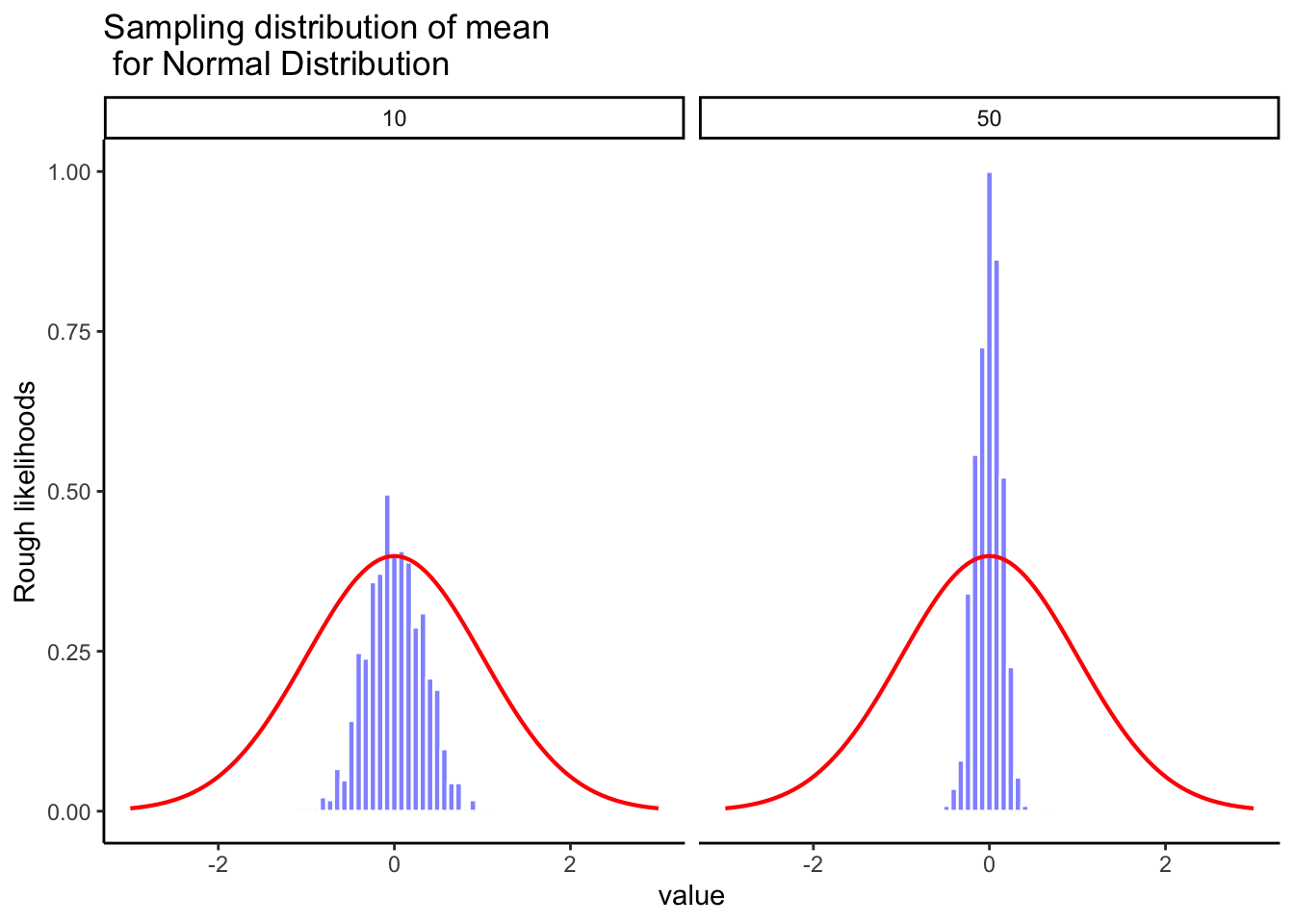
In Figure 4.13, we are smapling from a normal distribution (red line). The sampling distribution of the mean (blue bars) is also normal.

Figure 4.13: Sampling distributions of the mean from a normal population. As sample size increases, the distribution tightens around the population mean.

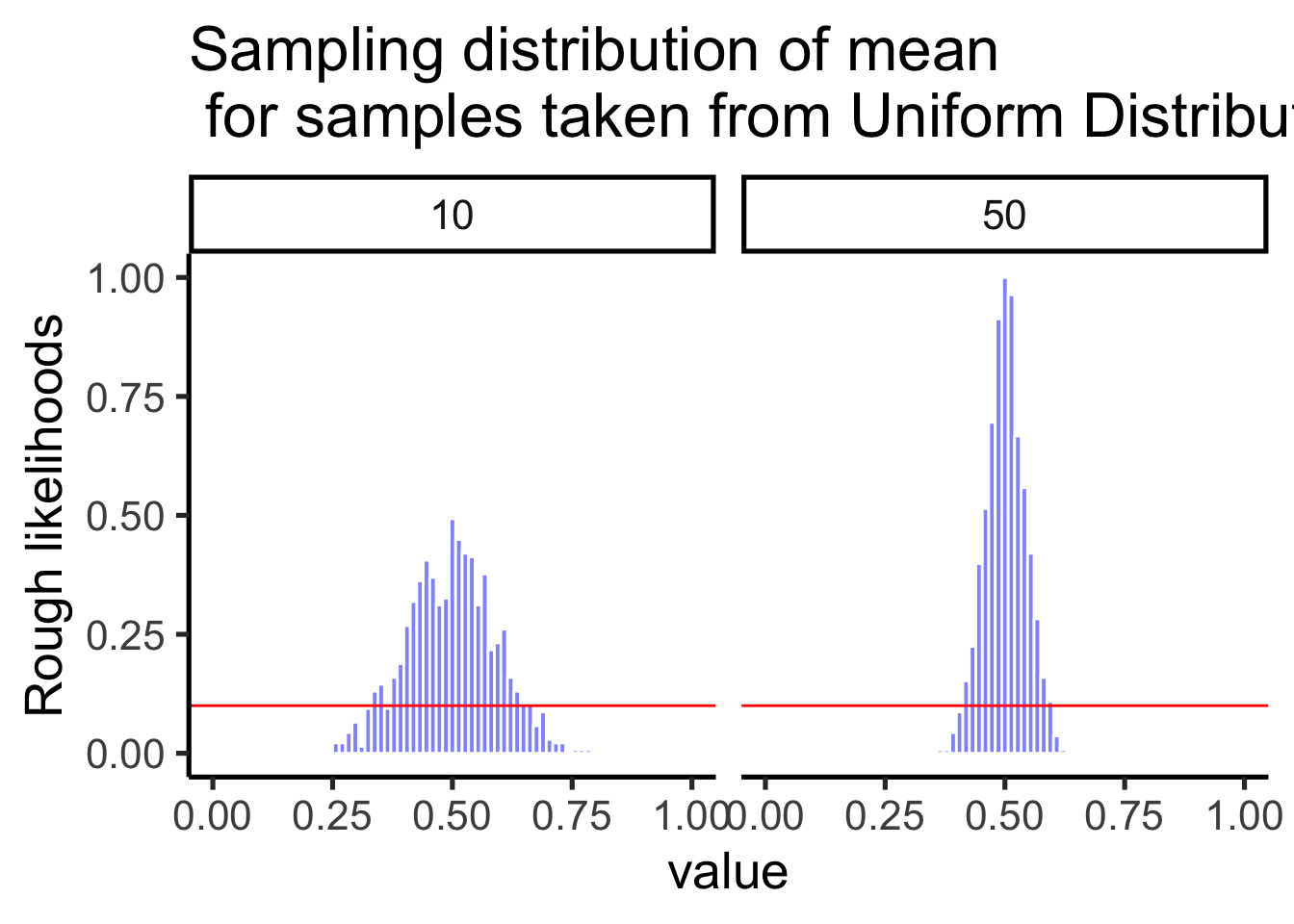
Let’s try sampling from a uniform population: the parent distribution is flat (red), but the sampling distribution of the mean is bell-shaped (Figure 4.14).

Figure 4.14: Even when samples come from a flat uniform distribution, the distribution of sample means is approximately normal.

Sampling from an exponential population: the parent distribution is skewed, but the sampling distribution of the mean still looks normal (Figure 4.15).

Figure 4.15: Even when samples come from a skewed exponential distribution, the distribution of sample means is approximately normal.

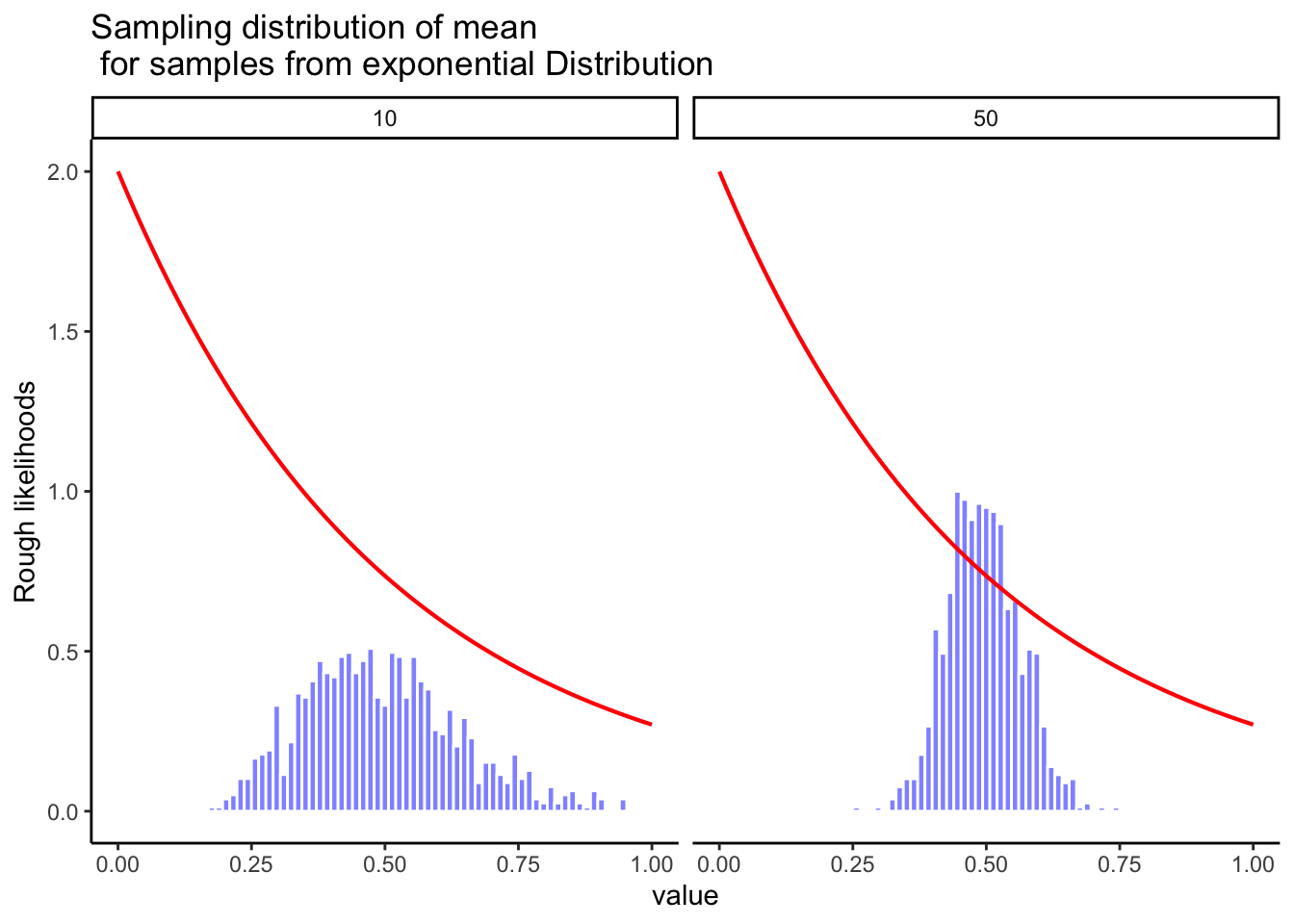
Together, these results are the essence of the central limit theorem (CLT). Formally, if the population has mean \(\mu\) and standard deviation \(\sigma\), then the sampling distribution of the mean also has mean \(\mu\) and standard error

\[SE = \frac{\sigma}{\sqrt{N}}.\]

This formula shows how sample size controls reliability. As \(N\) increases, the denominator grows and the SE falls. The drop is not linear: doubling \(N\) cuts the SE by only about 30%, which is why the benefits of ever-larger samples taper off. Still, larger samples consistently produce more stable and trustworthy estimates of \(\mu\).

The CLT is one of the cornerstones of statistics. It explains why sample means are useful, why bigger studies are more reliable, and why the normal curve appears so often in practice. Whenever you average across many influences, exam scores, crop yields, daily temperatures, the distribution of those averages tends to be normal.

4.12 z-scores

A z-score is a standardized way to express how far a value is from its mean, measured in units of standard deviation. Z-scores are useful because (i) areas under the normal curve translate directly into probabilities, and (ii) by the CLT, many averages (e.g., sample means) are approximately normal, so z-scores let us read off probabilities for those, too.

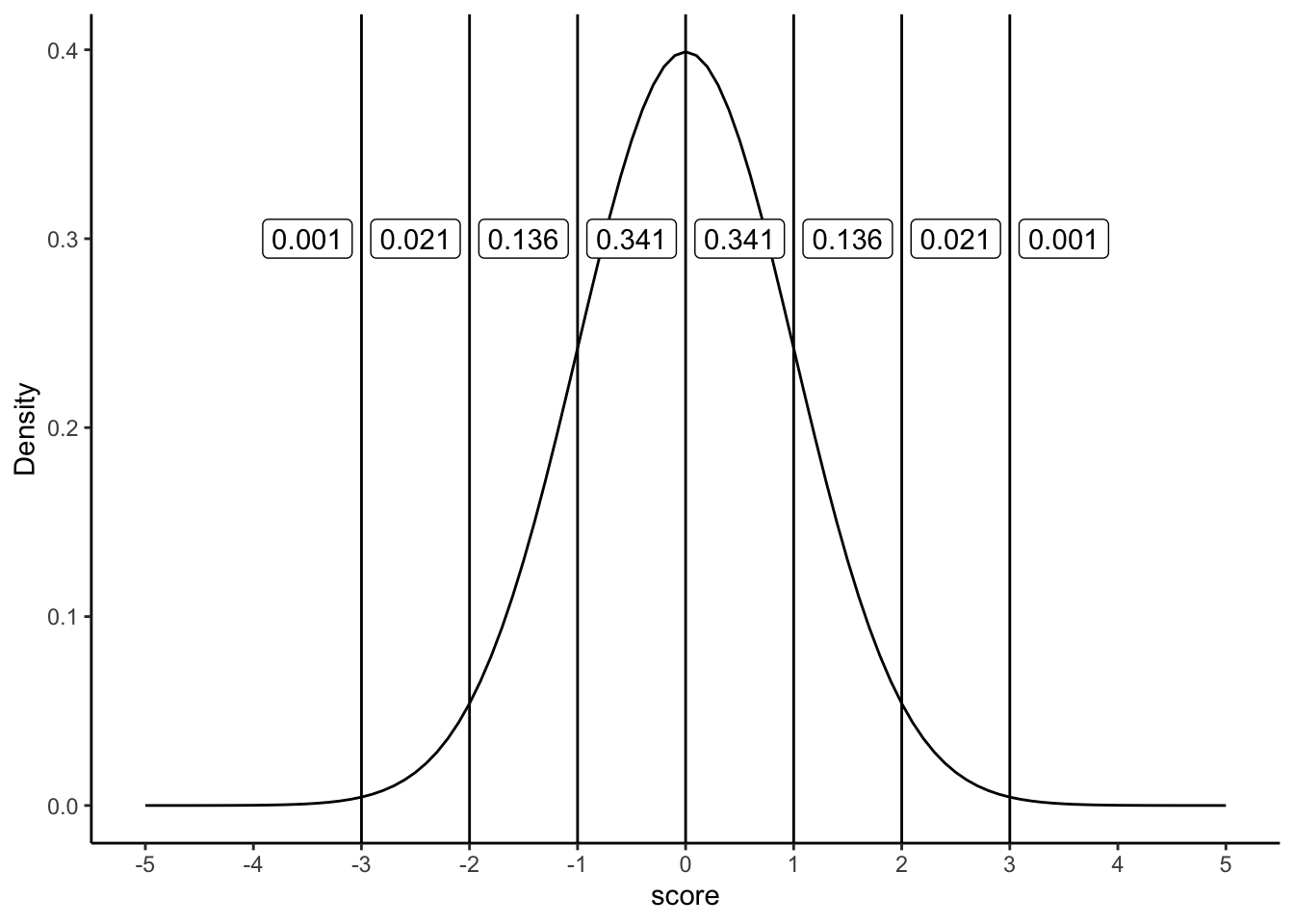
First, recall the geometry of the normal curve. In Figure 4.16 we draw vertical lines at 0, ±1, ±2, and ±3 standard deviations for a standard normal (\(\mu=0,\sigma=1\)). The labels show familiar areas: about 34.1% between 0 and 1, 13.6% between 1 and 2, and so on. Altogether, about 68.2% of values lie between −1 and +1 SD.

Figure 4.16: A normal distribution. Each line marks a standard deviation from the mean; labels show the proportion between adjacent lines.

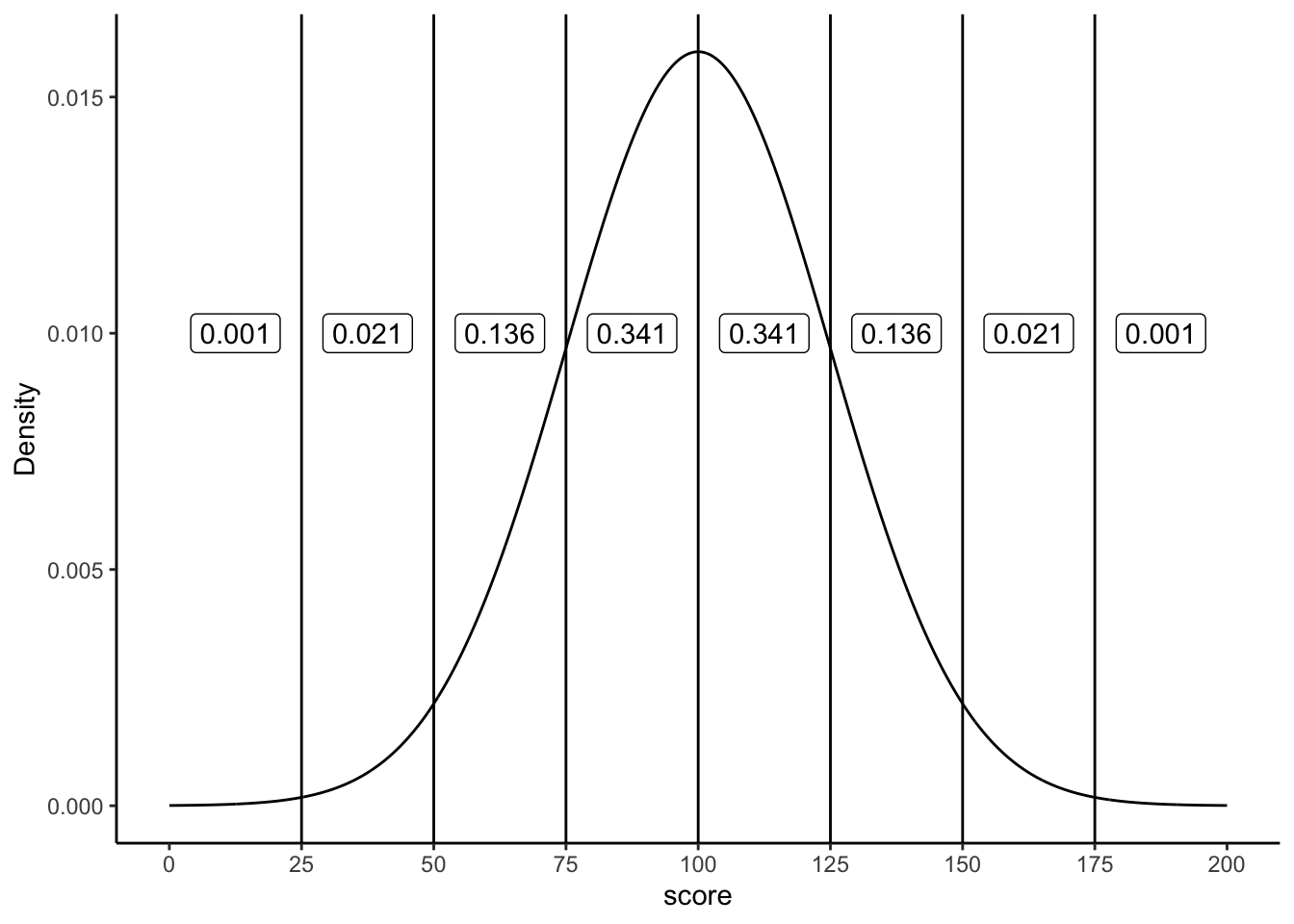
Those same proportions hold for any normal distribution, regardless of its mean or SD. In Figure 4.17 (with \(\mu=100,\ \sigma=25\)), the region from 100 to 125 (one SD above the mean) still contains about 34.1% of values.

Figure 4.17: The same area rules apply for any normal: one SD on either side covers ~68.2%, etc.

4.12.1 What “standardized” means

Standardizing converts raw scores to z-scores by subtracting the mean and dividing by the standard deviation:

\(z=\frac{x-\mu}{\sigma}\)

Interpretation is immediate: - z=0 is the mean, - z=1 is one SD above the mean, - z=-2 is two SDs below, etc.

Because z-scores put everything on the same scale, you can compare values across different normal variables (or read probabilities from the standard normal). And by the CLT, you can do the same with sample means when N is modestly large.

4.12.2 Calculating z-scores

If the population mean and SD are known, use them in the formula. In practice they’re often unknown, so we standardize with the sample mean x and sample SD s as estimates.

Example: generate ten observations from a \(N(100, 25^2)\) distribution, then standardize:

#> # A tibble: 10 × 2
#>    Observation Score
#>          <int> <dbl>
#>  1           1 122. 
#>  2           2 102. 
#>  3           3 113. 
#>  4           4  92.4
#>  5           5 103. 
#>  6           6 160. 
#>  7           7  86.4
#>  8           8  92.8
#>  9           9 115. 
#> 10          10  53.9

Using the known population values:

\((scores - 100)/25\)

#> # A tibble: 10 × 3
#>    Observation Score Zscore
#>          <int> <dbl>  <dbl>
#>  1           1 122.    0.88
#>  2           2 102.    0.1 
#>  3           3 113.    0.51
#>  4           4  92.4  -0.3 
#>  5           5 103.    0.13
#>  6           6 160.    2.41
#>  7           7  86.4  -0.54
#>  8           8  92.8  -0.29
#>  9           9 115.    0.6 
#> 10          10  53.9  -1.84

Once standardized, areas under the normal curve tell you how unusual a score is. z between −1 and 1 is common (~68% of cases), between 1 and 2 is less common (~13.6% on each side), and beyond ±2 is relatively rare (~2.1% in each tail segment between 2 and 3, even less beyond 3).

Finally, z-scores are also called standardized scores because they express distance from the mean in SD units.

4.13 Estimating population parameters

4.13.1 Why estimate? (two quick motivations)

• Concrete: A bootmaker wants the mean and spread of adult foot lengths to plan inventory. Measuring everyone is impossible; a well-designed sample can estimate those parameters closely enough to act on.

• Abstract: In experiments, we often ask whether a manipulation changes a response. Even if the broader “population” is fuzzy, we still estimate the mean response and its variability under each condition to compare them.

4.13.2 Sample statistic vs. estimate

A statistic describes your data; an estimate is your best guess about the corresponding population parameter. For the mean, these coincide:

Symbol	What is it?	Do we know it?
\(\bar{X}\)	Sample mean	Yes, calculated from the raw data
\(\mu\)	True population mean	Almost never known for sure
\(\hat{\mu}\)	Estimate of the population mean	Yes, for simple random samples \(\hat\mu=\bar X\)

4.13.3 Estimating the population standard deviation

Estimating the population mean was straightforward: the sample mean \(\bar X\) is an unbiased estimator of \(\mu\), meaning that across many samples it lands on the true mean on average. Standard deviation is trickier.

Here we encounter bias. An estimator is biased if its expected value systematically differs from the true population parameter. The sample standard deviation \(sd\) is such a case: it tends to underestimate \(\sigma\), especially when \(N\) is small.

That is why back in Chapter 2 we saw two formulas for the standard deviation, one dividing by \(N\) and one by \(N-1\). We can now explain why.

4.13.4 Simulating bias

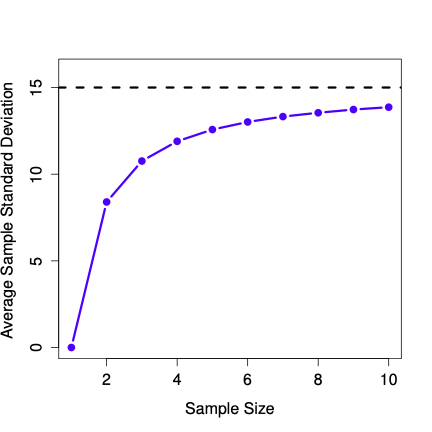
We can see this by creating a sampling distribution of the standard deviation. Suppose the true population IQ distribution has mean 100 and standard deviation 15. If we repeatedly draw small samples (say, \(N=2\)) and compute \(s\) each time, the histogram of those \(s\) values looks like Figure 4.18.

Figure 4.18: Sampling distribution of the sample standard deviation for N = 2. The true population SD is 15 (dashed line), but most experiments produce smaller values. The average sample SD is only 8.5, showing that \(s\) underestimates \(sigma\).

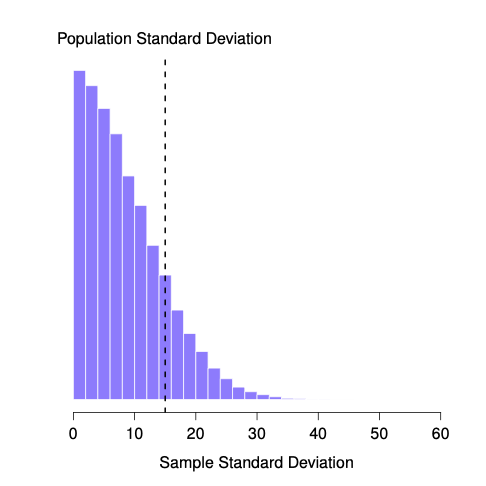
Even though the true \(\sigma\) is 15, the average sample SD is only about 8.5. This is very different from the sampling distribution of the mean, which is centered on \(\mu\).

If we repeat the simulation for a range of sample sizes, the contrast is clear:

• Figure 4.19 shows that the sample mean stays centered on \(\mu\) (unbiased).

• Figure 4.20 shows that the sample SD underestimates \(\sigma\) when \(N\) is small, though the bias shrinks as \(N\) grows.

Figure 4.19: The sample mean is an unbiased estimator of the population mean.

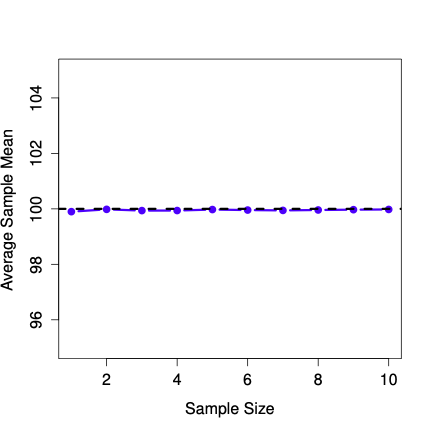
Figure 4.20 shows the sample standard deviation as a function of sample size. Unlike the mean, the sample standard deviation does not center on the population value. Small samples especially understate variability.

Figure 4.20: The sample standard deviation is a biased estimator of the population standard deviation.

4.13.5 Why variance needs a small correction

The reason comes from how variance is defined. The sample variance is

\[s^2 = \frac{1}{N}\sum_{i=1}^N (X_i-\bar X)^2.\]

On average, this formula underestimates the true variance \(\sigma^2\).

The standard fix is simple: divide by \(N-1\) instead of \(N\).

\[\hat\sigma^2 = \frac{1}{N-1}\sum_{i=1}^N (X_i-\bar X)^2.\]

This \(\hat\sigma^2\) is an unbiased estimator of \(\sigma^2\). For standard deviation, we use

\[\hat\sigma = \sqrt{\hat\sigma^2}.\]

Strictly, \(\hat\sigma\) is still slightly biased for \(\sigma\), but it is conventional and practically preferred.

Practice and terminology

• Software defaults: Some functions divide by \(N-1\), others by \(N\). Always check.

Terminology:

• \(s\) (divide by \(N\)): property of the sample, but biased for \(\sigma\).

• \(\hat\sigma\) (divide by \(N-1\)): estimate of the population SD.

In everyday analysis, most people report \(\hat\sigma\) but casually call it the “sample SD.” It’s fine in practice, but conceptually it’s worth keeping the distinction clear: \(s\) describes what you observed, while \(\hat\sigma\) is your best guess at the population’s variability.

Note

The \(N-1\) correction matters most for small samples. When \(N\) is large, the difference between dividing by \(N\) and \(N-1\) becomes negligible, since \(N\) and \(N-1\) are nearly the same. In practice, the correction only noticeably affects estimates when sample sizes are small.

To summarize:

Symbol	Definition	Known?
\(s^2\)	Sample variance (divide by \(N\))	Yes, calculated directly from data
\(\sigma^2\)	Population variance	No, almost never known exactly
\(\hat{\sigma}^2\)	Estimated population variance (divide by \(N-1\))	Yes, but distinct from \(s^2\)

4.14 Estimating a confidence interval

Statistics means never having to say you’re certain – Unknown origin

So far, we’ve focused on using sample data to estimate population parameters, but every estimate comes with some uncertainty. A single number, like “the mean IQ is 115,” doesn’t capture how confident we are. What we want is a range that likely contains the true population mean. That range is called a confidence interval (CI).

The Idea

Thanks to the central limit theorem, we know the sampling distribution of the mean is approximately normal. In a normal distribution, 95% of values fall within about 1.96 standard deviations of the mean.

If we knew the population mean and SD (\(\mu\), \(\sigma\))), the central limit theorem tells us where sample means tend to fall: a sample mean (\(\bar X\)) is usually within about (1.96) standard errors of (\(\mu\)), where

\(\text{SEM}=\frac{\sigma}{\sqrt{N}}\)

That’s the forward view (model → data).

In practice we want the reverse (data → model): given an observed (\(\bar X\)), what can we say about (\(\mu\))? Rearranging the same inequality gives

\[ \bar{X} - 1.96\,\frac{\sigma}{\sqrt{N}} \le \mu \le \bar{X} + 1.96\,\frac{\sigma}{\sqrt{N}} \]

so the 95% confidence interval is

\[ CI_{95} = \bar{X} \pm 1.96\,\frac{\sigma}{\sqrt{N}} \]

The constant (1.96) is the normal cutoff for 95%; for other levels use the corresponding normal quantile (e.g., (1.04) for 70%).

The catch

There’s one snag: this formula assumes we know the population standard deviation \(\sigma\). But in practice, \(\sigma\) is almost never known. We estimate it with \(\hat\sigma\), which introduces extra uncertainty.

To account for this, we swap the normal cutoffs for those from the \(t\)-distribution, which depends on sample size. With small \(N\), the \(t\) values are larger, so the CI widens. As \(N\) grows, \(t\) values shrink toward 1.96, and the \(t\)-based CI becomes indistinguishable from the normal version.

Tip

Rule of thumb: larger \(N\) → smaller SE → narrower CI.

Why it matters

Confidence intervals tell us how precise our guess is, and they force us to acknowledge uncertainty. A wide interval tells us we don’t have much precision; a narrow one suggests greater precision.

4.15 Chapter Summary

This chapter introduced the logic of sampling and estimation. We began with the basics of probability and probability distributions (with special focus on the normal distribution), then turned to the relationship between samples and populations and showed how repeated sampling leads to stable patterns. The law of large numbers explains why larger samples give more reliable estimates, and the sampling distribution of sample means shows how those estimates vary around the truth. The central limit theorem builds on this: the distribution of sample means centers on the population mean, narrows with larger \(N\), and tends toward normality.

Building on this theory, we turned to estimation of population parameters. The sample mean is an unbiased estimator of the population mean, but the sample standard deviation systematically underestimates the population spread. The \(N-1\) correction provides an unbiased variance estimator and the standard deviation estimate most researchers report. Finally, we introduced confidence intervals as a way to express the uncertainty around an estimate.

4.16 Videos

4.16.1 Introduction to Probability

Jeff has several more videos on probability that you can view on his statistics playlist.

4.16.2 Chebychev’s Theorem

4.16.3 Z-scores

4.16.4 Normal Distribution I

4.16.5 Normal Distribution II

Barnes, Mallory L. 2023. Statistics for Environmental Science.